Understanding Fractions: A Fun & Easy Guide for Students

Ever felt like fractions are frustrating? You're not alone! Many students struggle with these mathematical expressions, but they're actually one of the most practical math concepts you'll ever learn. Whether you're dividing pizza slices, measuring ingredients for a recipe, or calculating discounts while shopping, fractions are everywhere in daily life. In this comprehensive guide, we'll break down fractions into bite-sized pieces that are easy to understand and fun to learn.

What Are Fractions, Really?

At their core, fractions represent parts of a whole. Imagine a chocolate bar divided into 8 equal pieces. If you eat 3 pieces, you've consumed 3/8 of the chocolate bar. In this fraction:

• The number on top (3) is called the numerator - it tells you how many parts you have
• The number on the bottom (8) is called the denominator - it tells you how many equal parts make up the whole

Types of Fractions You Should Know

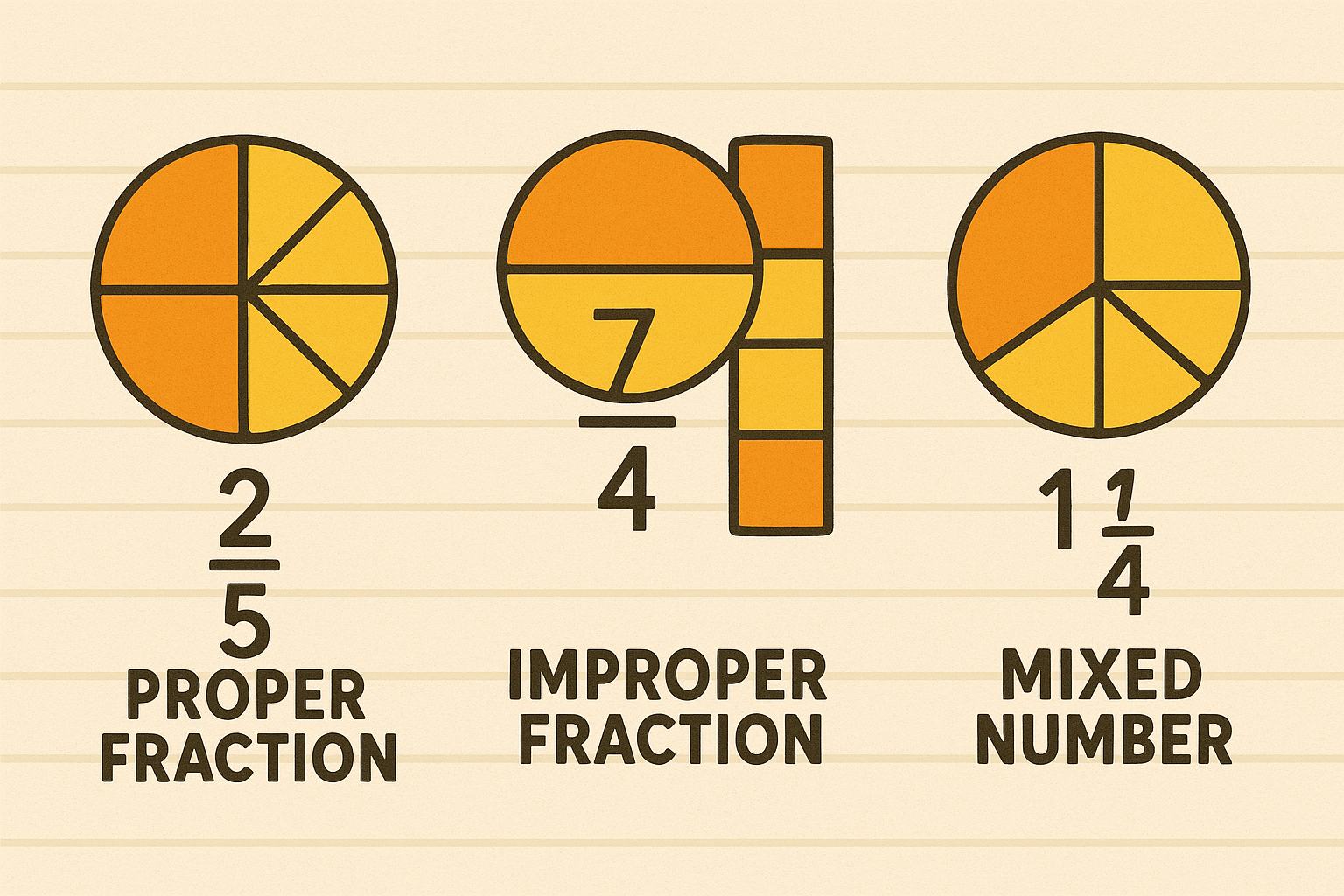
Proper Fractions

When the numerator is smaller than the denominator (like 2/5), you have a proper fraction. These fractions are always less than 1.

Improper Fractions

When the numerator is larger than or equal to the denominator (like 7/4), you have an improper fraction. These fractions are always greater than or equal to 1.

Mixed Numbers

A mixed number combines a whole number with a proper fraction (like 3½). It's another way to express improper fractions.

Converting Between Different Forms

Improper Fractions to Mixed Numbers

1. Divide the numerator by the denominator
2. The quotient becomes your whole number
3. The remainder becomes your new numerator
4. The denominator stays the same

Mixed Numbers to Improper Fractions

1. Multiply the whole number by the denominator
2. Add the numerator
3. Put this sum over the original denominator

The Four Basic Operations with Fractions

Addition and Subtraction

To add or subtract fractions, you need a common denominator first. Then:

1. Find the least common multiple (LCM) of the denominators
2. Convert each fraction to an equivalent fraction with the LCM as the denominator
3. Add or subtract the numerators
4. Simplify the result if possible

Multiplication

Multiplying fractions is straightforward:

1. Multiply the numerators together
2. Multiply the denominators together
3. Simplify if possible

Division

To divide fractions:

1. Take the second fraction and flip it (find its reciprocal)
2. Multiply by the first fraction
3. Simplify if possible

The Secret Sauce: Finding Equivalent Fractions

Equivalent fractions represent the same value but look different. To find equivalent fractions:

1. Multiply or divide both the numerator and denominator by the same non-zero number
2. The fraction value remains unchanged

Comparing Fractions: Which is Bigger?

Method 1: Cross Multiplication

1. Multiply the first numerator by the second denominator
2. Multiply the second numerator by the first denominator
3. Compare the products

Method 2: Convert to the same denominator and compare numerators

Real-World Applications of Fractions

Fractions aren't just abstract math concepts - they're incredibly practical:

• Cooking and Baking: Adjusting recipes requires understanding fractions (doubling a recipe that calls for ¾ cup of flour)
• Construction and Woodworking: Precise measurements often use fractions of inches
• Music: Note durations are expressed as fractions (quarter notes, half notes)
• Shopping: Calculating discounts (25% off = 1/4 off)
• Time Management: Portions of an hour (15 minutes = 1/4 hour)

Common Fraction Mistakes to Avoid

1. Adding denominators: Remember, 1/2 + 1/3 is NOT 2/5!
2. Forgetting to find common denominators before adding or subtracting
3. Canceling incorrectly when simplifying fractions
4. Mixing up multiplication and division rules

Challenge Yourself: SAT-Level Fraction Problems

Ready to test your fraction mastery with some challenging problems? Here are five medium to hard SAT-style questions that will put your skills to the test:

Ready to put your fraction skills to the test? Mathz AI's interactive tutor provides personalized practice to strengthen your understanding!

Conclusion

Fractions may seem intimidating at first, but with practice and the right approach, they become an essential tool in your mathematical toolkit. Remember that mastering fractions is like building with blocks - start with a solid foundation of understanding what fractions represent, then gradually build up to more complex operations.